树

更新9/20/2025

字数0

时长0 分钟

二叉树

二叉树（binary tree）是一种非线性数据结构，代表“祖先”与“后代”之间的派生关系，体现了“一分为二”的分治逻辑。与链表类似，二叉树的基本单元是节点，每个节点包含值、左子节点引用和右子节点引用

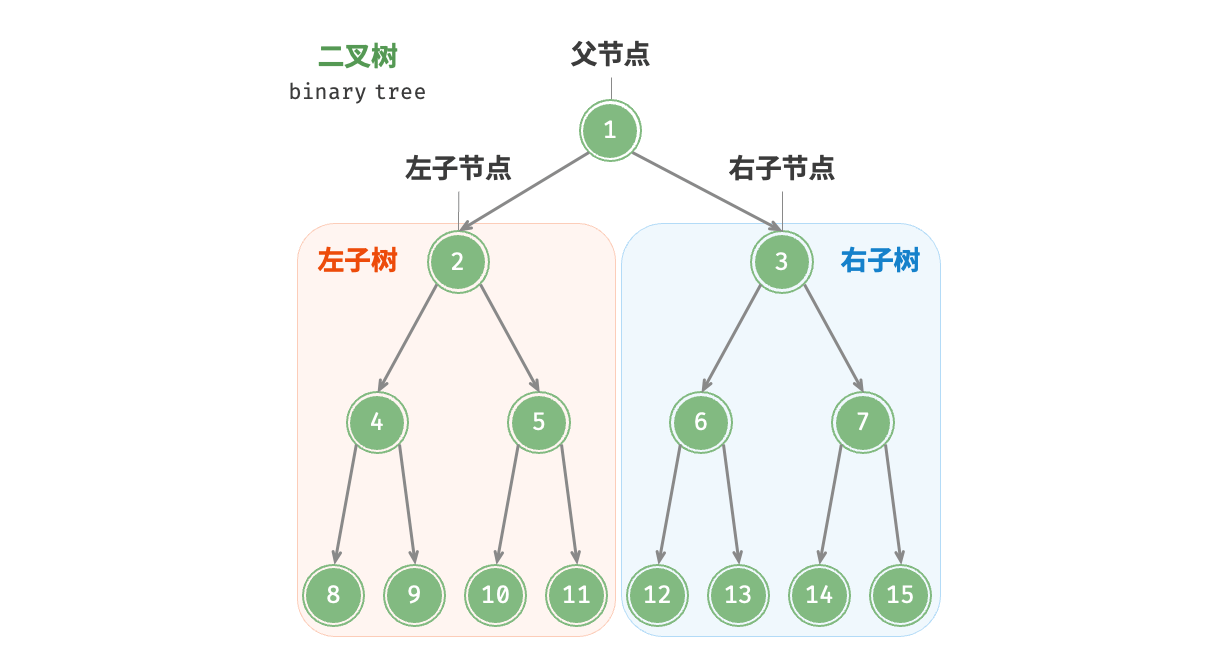
二叉树常见术语

• 根节点（root node）：位于二叉树顶层的节点，没有父节点。
• 叶节点（leaf node）：没有子节点的节点，其两个指针均指向 None 。
• 边（edge）：连接两个节点的线段，即节点引用（指针）。
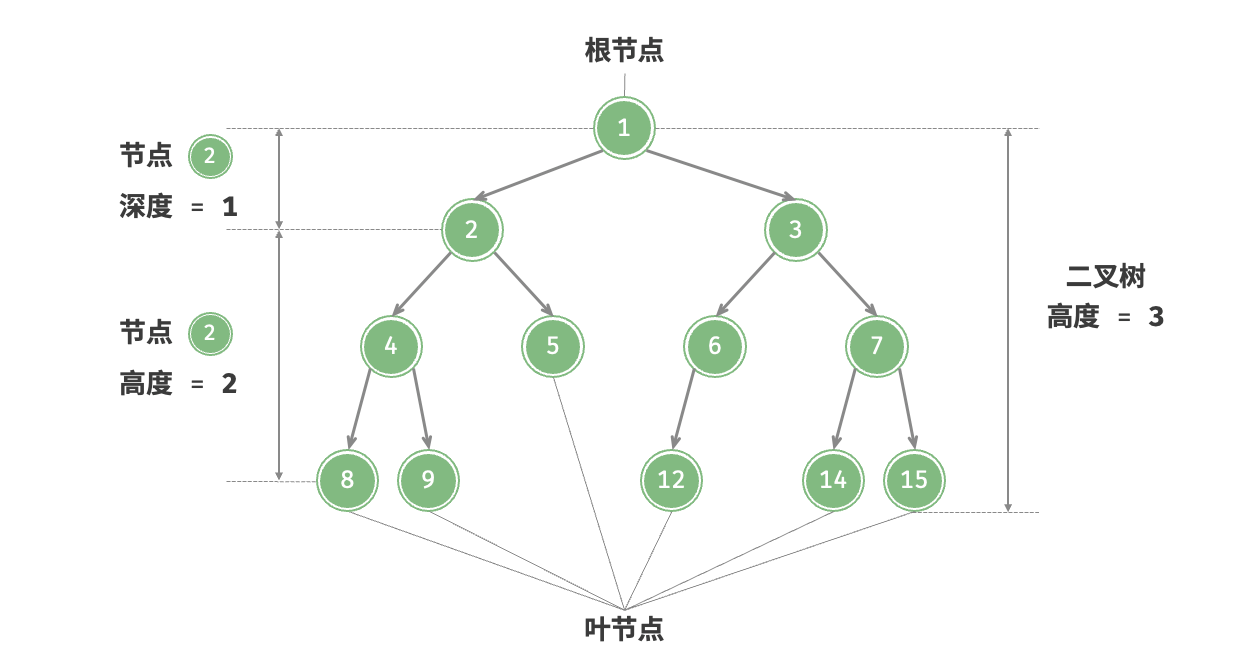
• 节点所在的层（level）：从顶至底递增，根节点所在层为 1 。
• 节点的度（degree）：节点的子节点的数量。在二叉树中，度的取值范围是 0、1、2 。
• 二叉树的高度（height）：从根节点到最远叶节点所经过的边的数量。
• 节点的深度（depth）：从根节点到该节点所经过的边的数量。
• 节点的高度（height）：从距离该节点最远的叶节点到该节点所经过的边的数量。

二叉树常见类型

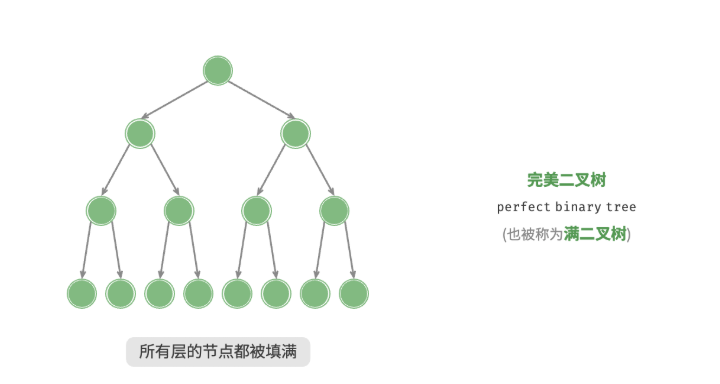
完美二叉树

完美二叉树 (perfect binary tree) 所有层的节点都被完全填满，在完美二叉树中，叶节点的度为 $0$，其余所有节点的度都为 $2$；若树的高度为 $h$，则节点总数为 $2^{h+1} - 1$，呈现标准的指数级关系，反映了自然界中常见的细胞分裂现象。

完全二叉树

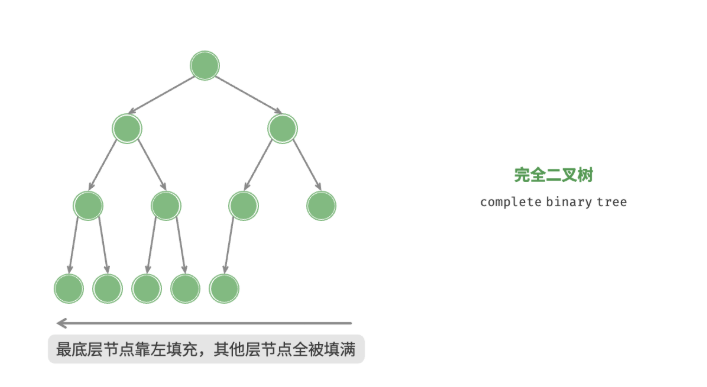
完全二叉树（complete binary tree）仅允许最底层的节点不完全填满，且最底层的节点必须从左至右依次连续填充。请注意，完美二叉树也是一棵完全二叉树。

完满二叉树

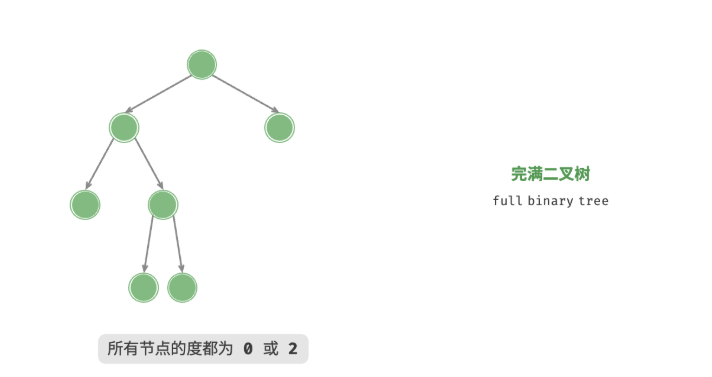
完满二叉树（full binary tree）除了叶节点之外，其余所有节点都有两个子节点。

平衡二叉树

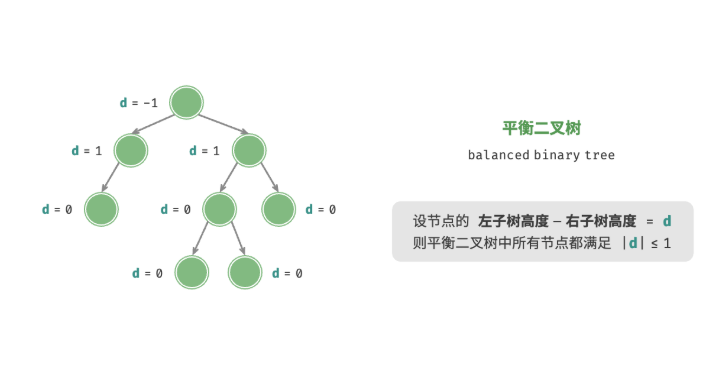
平衡二叉树（balanced binary tree）中任意节点的左子树和右子树的高度之差的绝对值不超过 1 。

二叉树遍历

深度优先遍历（DFS）

前序遍历（Pre-order）

• 访问顺序：根节点 → 左子树 → 右子树
• 应用：复制树结构、表达式求值的前缀表示

中序遍历（In-order）

• 访问顺序：左子树 → 根节点 → 右子树
• 应用：二叉搜索树的中序遍历可得到有序序列

后序遍历（Post-order）

• 访问顺序：左子树 → 右子树 → 根节点
• 应用：计算目录大小、删除树节点、表达式求值的后缀表示

代码实现

前序、中序和后序遍历都属于深度优先遍历（depth-first traversal），也称深度优先搜索（depth-first search, DFS），它体现了一种“先走到尽头，再回溯继续”的遍历方式。

/* 前序遍历 */
void preOrder(TreeNode root) {
    if (root == null)
        return;
    // 访问优先级：根节点 -> 左子树 -> 右子树
    list.add(root.val);
    preOrder(root.left);
    preOrder(root.right);
}

/* 中序遍历 */
void inOrder(TreeNode root) {
    if (root == null)
        return;
    // 访问优先级：左子树 -> 根节点 -> 右子树
    inOrder(root.left);
    list.add(root.val);
    inOrder(root.right);
}

/* 后序遍历 */
void postOrder(TreeNode root) {
    if (root == null)
        return;
    // 访问优先级：左子树 -> 右子树 -> 根节点
    postOrder(root.left);
    postOrder(root.right);
    list.add(root.val);
}

广度优先遍历（BFS）

层序遍历（Level-order）

• 访问顺序：按层级从上到下、从左到右逐层访问
• 实现方式：通常使用队列
• 应用：寻找最短路径、打印树的层级结构

代码实现

广度优先遍历通常借助“队列”来实现。队列遵循“先进先出”的规则，而广度优先遍历则遵循“逐层推进”的规则，两者背后的思想是一致的

/* 层序遍历 */
List<Integer> levelOrder(TreeNode root) {
    // 初始化队列，加入根节点
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    // 初始化一个列表，用于保存遍历序列
    List<Integer> list = new ArrayList<>();
    while (!queue.isEmpty()) {
        TreeNode node = queue.poll(); // 队列出队
        list.add(node.val);           // 保存节点值
        if (node.left != null)
            queue.offer(node.left);   // 左子节点入队
        if (node.right != null)
            queue.offer(node.right);  // 右子节点入队
    }
    return list;
}

构造二叉树

从前序与中序遍历序列构造二叉树

class Solution {
    private Map<Integer, Integer> indexMap;

    // 递归构造二叉树
    public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
        if (preorder_left > preorder_right) {
            return null;
        }

        // 前序遍历中的第一个节点就是根节点
        int preorder_root = preorder_left;
        // 在中序遍历中定位根节点
        int inorder_root = indexMap.get(preorder[preorder_root]);
        
        // 先把根节点建立出来
        TreeNode root = new TreeNode(preorder[preorder_root]);
        // 得到左子树中的节点数目
        int size_left_subtree = inorder_root - inorder_left;
        // 递归地构造左子树，并连接到根节点
        // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
        root.left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
        // 递归地构造右子树，并连接到根节点
        // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
        root.right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
        return root;
    }

    // 入口方法
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        // 构造哈希映射，帮助我们快速定位根节点
        indexMap = new HashMap<Integer, Integer>();
        for (int i = 0; i < n; i++) {
            indexMap.put(inorder[i], i);
        }
        return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
    }
}

二叉搜索树

二叉搜索树（binary search tree）满足以下条件。

• 对于根节点，左子树中所有节点的值 根节点的值 右子树中所有节点的值。
• 任意节点的左、右子树也是二叉搜索树，即同样满足条件 1. 。

二叉搜索树的操作

查找节点

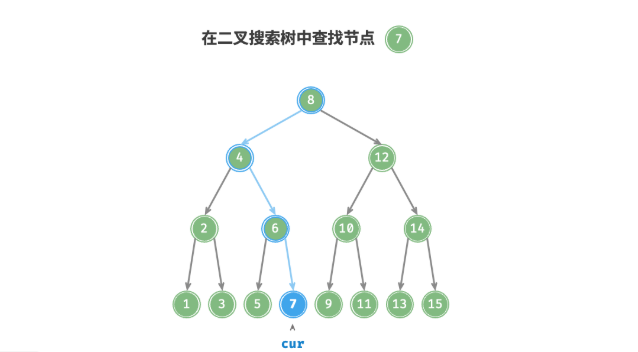
给定目标节点值 num ，可以根据二叉搜索树的性质来查找。如图 7-17 所示，我们声明一个节点 cur ，从二叉树的根节点 root 出发，循环比较节点值 cur.val 和 num 之间的大小关系。

• 若 cur.val < num ，说明目标节点在 cur 的右子树中，因此执行 cur = cur.right 。
• 若 cur.val > num ，说明目标节点在 cur 的左子树中，因此执行 cur = cur.left 。
• 若 cur.val = num ，说明找到目标节点，跳出循环并返回该节点。

/* 查找节点 */
TreeNode search(int num) {
    TreeNode cur = root;
    // 循环查找，越过叶节点后跳出
    while (cur != null) {
        // 目标节点在 cur 的右子树中
        if (cur.val < num)
            cur = cur.right;
        // 目标节点在 cur 的左子树中
        else if (cur.val > num)
            cur = cur.left;
        // 找到目标节点，跳出循环
        else
            break;
    }
    // 返回目标节点
    return cur;
}

插入节点

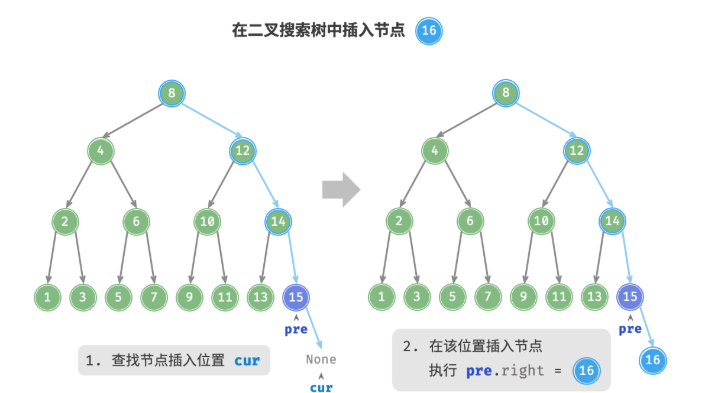
1. 查找插入位置：与查找操作相似，从根节点出发，根据当前节点值和 num 的大小关系循环向下搜索，直到越过叶节点（遍历至 None ）时跳出循环。
2. 在该位置插入节点：初始化节点 num ，将该节点置于 None 的位置。

/* 插入节点 */
void insert(int num) {
    // 若树为空，则初始化根节点
    if (root == null) {
        root = new TreeNode(num);
        return;
    }
    TreeNode cur = root, pre = null;
    // 循环查找，越过叶节点后跳出
    while (cur != null) {
        // 找到重复节点，直接返回
        if (cur.val == num)
            return;
        pre = cur;
        // 插入位置在 cur 的右子树中
        if (cur.val < num)
            cur = cur.right;
        // 插入位置在 cur 的左子树中
        else
            cur = cur.left;
    }
    // 插入节点
    TreeNode node = new TreeNode(num);
    if (pre.val < num)
        pre.right = node;
    else
        pre.left = node;
}

删除节点

先在二叉树中查找到目标节点，再将其删除。与插入节点类似，我们需要保证在删除操作完成后，二叉搜索树的“左子树 < 根节点 < 右子树”的性质仍然满足。因此，我们根据目标节点的子节点数量，分 0、1 和 2 三种情况，执行对应的删除节点操作。

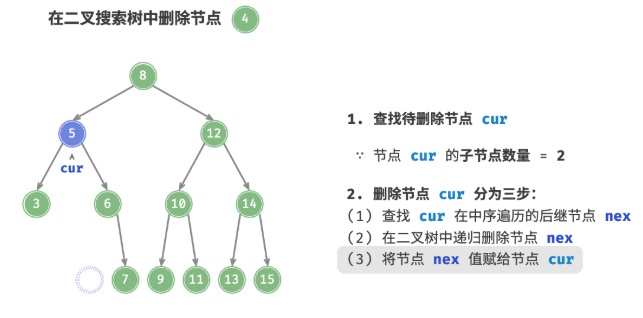
• 当待删除节点的度为 0 时，表示该节点是叶节点，可以直接删除。
• 当待删除节点的度为 1 时，将待删除节点替换为其子节点即可。
• 当待删除节点的度为 时，我们无法直接删除它，而需要使用一个节点替换该节点。由于要保持二叉搜索树“左子树 根节点 右子树”的性质，因此这个节点可以是右子树的最小节点或左子树的最大节点。

/* 删除节点 */
void remove(int num) {
    // 若树为空，直接提前返回
    if (root == null)
        return;
    TreeNode cur = root, pre = null;
    // 循环查找，越过叶节点后跳出
    while (cur != null) {
        // 找到待删除节点，跳出循环
        if (cur.val == num)
            break;
        pre = cur;
        // 待删除节点在 cur 的右子树中
        if (cur.val < num)
            cur = cur.right;
        // 待删除节点在 cur 的左子树中
        else
            cur = cur.left;
    }
    // 若无待删除节点，则直接返回
    if (cur == null)
        return;
    // 子节点数量 = 0 or 1
    if (cur.left == null || cur.right == null) {
        // 当子节点数量 = 0 / 1 时， child = null / 该子节点
        TreeNode child = cur.left != null ? cur.left : cur.right;
        // 删除节点 cur
        if (cur != root) {
            if (pre.left == cur)
                pre.left = child;
            else
                pre.right = child;
        } else {
            // 若删除节点为根节点，则重新指定根节点
            root = child;
        }
    }
    // 子节点数量 = 2
    else {
        // 获取中序遍历中 cur 的下一个节点
        TreeNode tmp = cur.right;
        while (tmp.left != null) {
            tmp = tmp.left;
        }
        // 递归删除节点 tmp
        remove(tmp.val);
        // 用 tmp 覆盖 cur
        cur.val = tmp.val;
    }
}

中序遍历有序

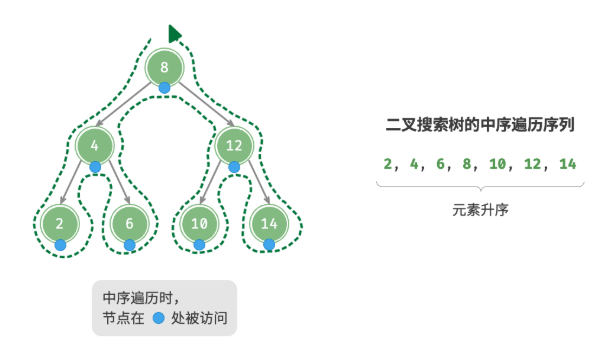
二叉树的中序遍历遵循 左 ->根 -> 右 的遍历顺序，而二叉搜索树满足 左子节点 -> 根节点 -> 右子节点”的大小关系。

这意味着在二叉搜索树中进行中序遍历时，总是会优先遍历下一个最小节点，从而得出一个重要性质：二叉搜索树的中序遍历序列是升序的。

二叉搜索树的效率

给定一组数据，我们考虑使用数组或二叉搜索树存储。二叉搜索树的各项操作的时间复杂度都是对数阶，具有稳定且高效的性能。只有在高频添加、低频查找删除数据的场景下，数组比二叉搜索树的效率更高。

	无序数组	二叉搜索树
查找元素	$O(n)$	$O(log n)$
插入元素	$O(1)$	$O(log n)$
删除元素	$O(n)$	$O(log n)$

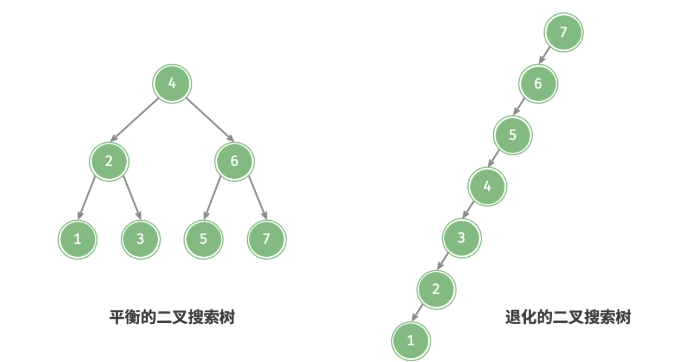
在理想情况下，二叉搜索树是“平衡”的，这样就可以在$O(log n)$ 轮循环内查找任意节点。

然而，如果我们在二叉搜索树中不断地插入和删除节点，可能导致二叉树退化成链表，这时各种操作的时间复杂度也会退化为$O(n)$。